VARIEDADE, SUPERFÍCIES, ESPAÇO TENSORIAL DIMENSIONAL GRACELI

VARIEDADE, SUPERFÍCIES, ESPAÇOS TENSORIAL DIMENSIONAL GRACELI.

Em matemática e física, um espaço de De Sitter é o análogo do espaço de Minkowski, ou de uma variedade quadrimensional de espaço-tempo, de uma esfera no comum espaço euclidiano. Também do ponto de vista geométrico, em certas classes de variedades lorentzianas, os espaços de Sitter e anti-de Sitter são os seus parentes mais próximos.[1] Isto significa que o espaço de de Sitter pode ser construído independentemente de qualquer teoria gravitacional, sendo portanto mais fundamental do que a equação de Einstein. Consequentemente, torna-se possível construir uma relatividade especial baseada no grupo de de Sitter, que e o grupo cinemático do espaço de de Sitter.[2] O espaço de De Sitter tem curvatura negativa constante -12/R2 (o sinal depende de convenções) e reproduz (após uma renormalização) o espaço-tempo de Minkowski no limite da curvatura zero.[3]

Definição

O espaço de De Sitter pode ser definida como uma subvariedade de um espaço de Minkowski de uma dimensão superior. Tome o espaço de Minkowski R1,n com a métrica padrão:

ds^{2}=-dx_{0}^{2}+\sum _{i=1}^{n}dx_{i}^{2}.

+

T^{\nu }{}_{\alpha }

[DR] =

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

\eta _{\mu \nu }

+ [

G_{\mu \nu }\

T_{\mu \nu }

T^{\nu }{}_{\alpha }

[DR] =

{\hat {H}}

\left|\psi ({\vec {r}},t)\right\rangle

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

-i\hbar {\frac {\partial }{\partial x_{n}}}

.

\left|\psi ({\vec {r}},t)\right\rangle

]

espaço de de Sitter é o subvariedade descrita pela hiperbolóide de uma folha

-x_{0}^{2}+\sum _{i=1}^{n}x_{i}^{2}=\alpha ^{2}

+

T^{\nu }{}_{\alpha }

[DR] =

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

\eta _{\mu \nu }

= + [

G_{\mu \nu }\

T_{\mu \nu }

T^{\nu }{}_{\alpha }

[DR] =

{\hat {H}}

\left|\psi ({\vec {r}},t)\right\rangle

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

-i\hbar {\frac {\partial }{\partial x_{n}}}

.

\left|\psi ({\vec {r}},t)\right\rangle

]

onde $\alpha$ é uma constante diferente de zero com as dimensões de comprimento. A métrica no espaço de Sitter é a métrica induzida da métrica de Minkowski ambiente.

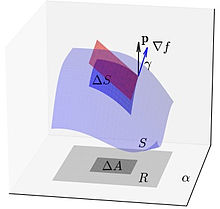
Uma integral de superfície é uma generalização das integrais múltiplas sobre uma superfície.[1][2][3] Dada uma superfície S, pode-se integrar sobre ela um campo escalar ou um campo vetorial. Aplicações de integrais de superfícies aparecem em vários ramos da ciência e das engenharias, tais como em problemas envolvendo fluxo de fluido e de calor, eletricidade, magnetismo, massa e centro de gravidade.[4] Por exemplo, ao integrarmos uma função densidade de massa sobre uma superfície, obteremos a massa aplicada sobre a superfície.[2] Em uma superfície orientável, a integral de superfície do produto interno de um campo vetorial pelo campo normal à superfície fornece o fluxo desse campo, indicado por pela letra grega maiúscula Φ.[3]

Definição

Seja $g: \mathbb{R}^3\to \mathbb{R}$ , $g = g(x,y,z)$ , uma função definida em todos os pontos de uma superfície $S$ . A integral de superfície de $g$ sobre $S$ é definida por[2]:

\int \int _{S}gd\sigma

T^{\nu }{}_{\alpha }

onde, $d\sigma$ é o elemento infinitesimal de área sobre a superfície.

Se $S$ é uma superfície orientável, então definimos a integral de superfície de um campo vetorial $F$ sobre $S$ por[3]:

\int \int _{S}\mathbf {F} \cdot \mathbf {n} d\sigma

T^{\nu }{}_{\alpha }

onde, $\mathbf {n}$ é o campo normal escolhido na orientação da superfície. O integrando na forma de produto escalar evidencia que somente as componentes do campo perpendiculares à superfície $S$ contribuirão no cálculo do fluxo.[4]

Orientação

Assim como as curvas, também as superfícies precisam ser orientadas, a fim de que, ao adotar certa convenção, sempre se encontre o mesmo sinal para fluxo Φ. Diz-se que uma superfície de dois lados é orientável e que uma superfície de um único lado é não orientável. Assim, existe a necessidade de distinção dos lados de uma superfície orientável e convenção para orientação considerada positiva e negativa, pois ao inverter a orientação de S inverte-se o sinal de Φ.[4]

Sendo assim:

O sinal de ${\overrightarrow {n}}$ serve para orientar $S$ .

Para o cálculo de ${\overrightarrow {n}}$ :
Suponha que a superfície $S$ seja dada como: $z=g(x,y)$ ou $y=g(x,z)$ ou $x=g(y,z)$ .
Reescrevendo cada uma das equações na forma $G(x,y,z)=0$ é possível interpretar a última como a equação de uma superfície de nível de uma função $w=G(x,y,z)$ .
A partir do conceito que ${\overrightarrow {\nabla }}G$ é um vetor 3-D e representa um vetor normal à superfície de nível $G(x,y,z)=0$ , pode-se definir ${\overrightarrow {n}}$ da seguinte forma:

{\overrightarrow {n}}={\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}

{\overrightarrow {n}}=-{\frac {{\overrightarrow {\nabla }}G}{|{\overrightarrow {\nabla }}G|}}

+

T^{\nu }{}_{\alpha }

G_{\mu \nu }\

Elemento de área

Elemento de área de uma superfície lisa.

O cálculo do elemento infinitesimal de área sobre a superfície pode ser feito com o auxílio de uma projeção adequada da superfície ${\textstyle S}$ sobre um plano do espaço cartesiano. Suponhamos que ${\textstyle S}$ é descrita pela superfície de nível $f(x,y,z) = c$ . Consideremos, ainda, um plano dado ${\textstyle \alpha}$ de normal unitária $\mathbf {p}$ . A projeção de $S$ sobre $\alpha$ define uma região planar que denotaremos por ${\textstyle R}$ .

Com isso, aproximamos um elemento de área $\Delta S$ da superfície $S$ pela área do elemento tangente associado. Este, por sua vez, pode ser calculado em função do elemento de área $\Delta S$ projetado sobre o plano $\alpha$ . Denotando este por $\Delta A$ , temos[2]:

\Delta S\approx {\frac {1}{|\cos \gamma |}}\Delta A

G_{\mu \nu }\

onde, $\gamma$ é o ângulo entre o vetor gradiente $\nabla f$ e o vetor $\mathbf {p}$ calculado em algum ponto de $\Delta S$ .

Assim, podemos calcular o elemento de área $d\sigma$ por[2]:

d\sigma = \frac{1}{|\cos \gamma|} dA

G_{\mu \nu }\

onde, $\gamma$ é o ângulo entre o vetor gradiente $\nabla f$ e o vetor $\mathbf {p}$ . $dA$ é o elemento de área planar.

Observamos, ainda, que o ângulo $\gamma$ está relacionado ao produto interno entre $\nabla f$ e $\mathbf {p}$ por:

\nabla f\cdot \mathbf {p} =|\nabla f||\mathbf {p} |\cos \gamma

T^{\nu }{}_{\alpha }

G_{\mu \nu }\

Segue, daí, que o elemento de área $d\sigma$ pode ser calculado por:

d\sigma ={\frac {|\nabla f||\mathbf {p} |}{|\nabla f\cdot \mathbf {p} |}}dA

T^{\nu }{}_{\alpha }

Teorema

Seja $S$ uma superfície suave da forma $z=g(x,y)$ ou $y=g(x,z)$ ou $x=g(y,z)$ e seja ${\overrightarrow {F}}$ um campo vetorial contínuo em $S$ . Supondo também que a equação de $S$ seja reescrita como $G(x,y,z)=0$ , ao passar $g$ para o membro esquerdo da equação e seja $R$ a projeção de $S$ no plano coordenado das variáveis independentes de $g$ .[4] Então:

\phi =\int \int _{S}{\overrightarrow {F}}\bullet {\overrightarrow {n}}dS=\pm \int \int _{R}{\overrightarrow {F}}\bullet {\overrightarrow {\nabla }}GdA

T^{\nu }{}_{\alpha }

SISTEMA GRACELI DE GEOMETRIA, TOPOLOGIA, E CÁLCULO E FÍSICA DE ESPAÇO TENSORIAL E DIMENSIONAL .

QUE PODE SER REPRESNETADO RELAÇÕES ENTRE ESPAÇOS E VARIAÇÕS NO TEMPO, TENSORES E DIMENSÕES, E DIMENSÕES E TENSORES DE GRACELI,

COMO EXEMPLO PODE-SE CITAR.

FÍSICA GRACELI TENSORIAL QUÂNTICA.

$equação Graceli quântica []$

$\psi ^{*}$

equação Graceli tensorial quântica [1]

$G_{\mu \nu }\$

$T_{\mu \nu }$ = tensor energia momentum

$G_{\mu \nu }\$ = tensor quântico de Graceli.

$equação Graceli tensorial quântica [2]$

$G_{\mu \nu }\$

$\psi ^{*}$

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ =

G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ =

EQUAÇÃO QUÂNTICA TENSORIAL GRACELI.

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ [DR] = ${\hat {H}}$ $\left|\psi ({\vec {r}},t)\right\rangle$ $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$

G $T^{\nu }{}_{\alpha }$ [DR] = É O TENSOR GRACELI TENSÃO ENERGIA DE FLUXOS DE DILATAÇÕES E RETRAÇÕES COM CURVATURAS E SIMÉTRICO .

G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ =

G $T^{\nu }{}_{\alpha }$ [DR] = É O TENSOR GRACELI TENSÃO ENERGIA DE FLUXOS DE DILATAÇÕES E RETRAÇÕES COM CURVATURAS E SIMÉTRICO .

$P^{\mu }\!$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$

ESPIRAL ESPAÇO-TEMPORAL.

GEOMETRIA, TOPOLOGIA , TOPOGEOMETRIA GRACELI DE REDES N-DIMENSIAL.

DIAGRAMA N-DIMENSIONAL DE REDES.

Sphere Points GIF - Sphere Points Connections GIFs

tumblr_nhkwnbESwu1rv33k2o5_500

Pesquisar este blog

VARIEDADE, SUPERFÍCIES, ESPAÇO TENSORIAL DIMENSIONAL GRACELI

Definição

Definição

Orientação

Elemento de área

Teorema

Comentários

Postar um comentário

Postagens mais visitadas deste blog